皆さん、こんにちは。システム商品開発グループの入澤です。
今冬は日本海側で寒波が襲来して、北陸らしい雪景色の中で過ごしておりました。ここ最近は寒さが緩んで雪解けが進んでいます。

さて、ブログタイトルにもある通りプログラマーの仕事で頻繁に出くわす高校数学のお話をもう少し続けてみたいと思います。前回「直線」を取り上げたときに、グラフィクスに関わるなら手足のように扱えなければならないと書きました。今回はもう一歩進んで「三角形」と「円」を見てみます。義務教育から嫌というほど関わってきたこれらもプログラマーにとって「直線」と同じく向き合わなければならない対象です。とくにグラフィクスでは、点の集まり、多角形（クローズパス）、連続線分（オープンパス）などベクタ形式のパスを計算する上で三角形と円の性質を多く使います。

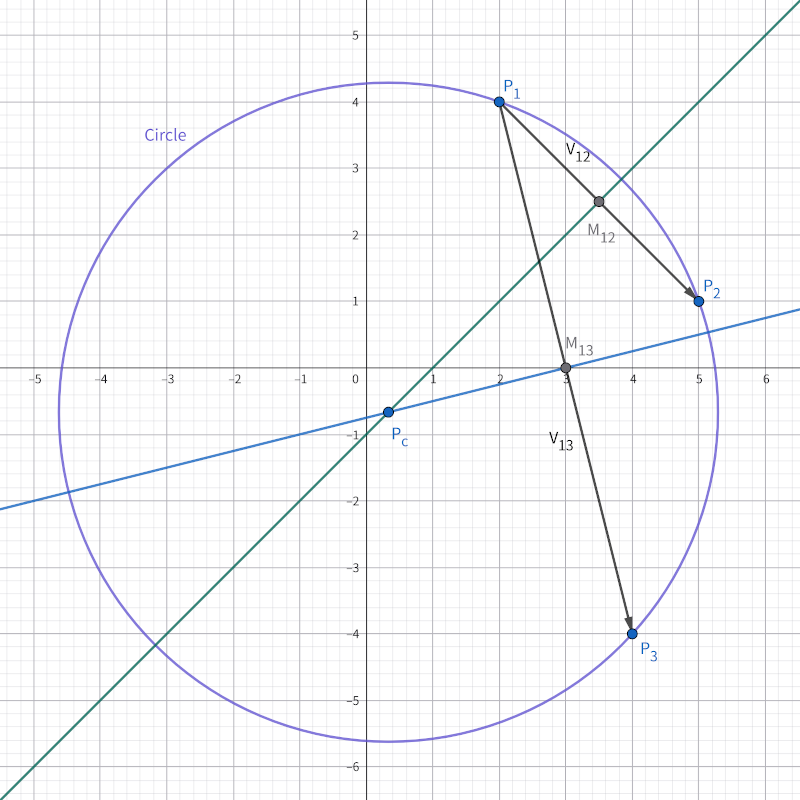
前提として、3つの頂点で与えられる三角形を考える場合がほとんどですから、${\displaystyle P_1=(x_1,y_1)}$、${\displaystyle P_2=(x_2,y_2)}$、${\displaystyle P_3=(x_3,y_3)}$ の座標を順番に与えておきます（今回も平面で考えます）。ここからまずは三角形の符号付き面積を計算してみましょう。三角形の頂点が時計回りか反時計回りかを判断できるので符号付きにします。方法はいくつもありますが、外積の性質（2つのベクトルの外積の成分はベクトルを平行移動して作る平行四辺形の面積に等しい）を使うと次の式が簡便です。

${\displaystyle S_{123}=\frac{1}{2}\{(x_2-<!--\; -\; -->x_1)(y_3-<!--\; -\; -->y_1)-<!--\; -\; -->(x_3-<!--\; -\; -->x_1)(y_2-<!--\; -\; -->y_1)\}}$   ...   Eq.1

絶対値 ${\displaystyle |S_{123}|}$ を計算することで面積が得られ、ゼロと比べることで3つの頂点の関係性が分かります。

• ${\displaystyle S_{123}<0}$ : 3つの頂点を ${\displaystyle P_1}$ → ${\displaystyle P_2}$ → ${\displaystyle P_3}$ で辿ると時計回りの順番になる（右手系）
• ${\displaystyle S_{123}=0}$ : 3つの頂点が一直線上に並んでいる
• ${\displaystyle S_{123}>0}$ : 3つの頂点は反時計回りの順番になる

少し具体的な応用を見てみると、多角形の符号付き面積、多角形の重心（幾何中心）、多角形の凸性判定などを計算するときに、多角形の頂点を辿りながら三角形のこの性質を上手く組み合わせて求めるのが常套手段です。

さて、Eq.1をよく見てみると行列式を使って次のようにも表せます。

${\displaystyle S_{123}=\frac{1}{2}\left|\begin{array}{cc}{x}_2-<!--\; -\; -->x_1& y_2-<!--\; -\; -->y_1\\ x_3-<!--\; -\; -->x_1& y_3-<!--\; -\; -->y_1\end{array}\right|=\frac{1}{2}\left|\begin{array}{ccc}{x}_1& y_1& 1\\ x_2& y_2& 1\\ x_3& y_3& 1\end{array}\right|}$   ...   Eq.2

2×2の行列式が行ベクトルで張られる平行四辺形の面積（3×3の行列式が行ベクトルで張られる平行六面体の体積）であるという幾何学的な意味から関係性をとらえることもできますし、行ベクトル（転置すれば列ベクトル）が線形独立か線形従属かを判定する式と見なすこともできます。まあ、わざわざ行列式で書いたのには訳がありまして、円が絡むときも登場するからです。

こんにちは。プリントソリューションGのTです。

2月14日はバレンタインデー
今年は14日が土曜日でしたので、前日の13日には
男性社員のデスクにカラフルな紙袋が置かれていました。

そして嬉しいことに……今年も早瀬浦の日本酒チョコをいただきました
いただいたチョコを次の週で少しずついただくのが毎年楽しみです。

甘いものを食べて、しっかりパワーを充電！
糖分をエネルギーに変えて、これからも頑張って仕事をしていきます！

こんにちは

今朝はお弁当作りでバタバタなスタートでした。
隙間に何を入れようかと悩んでいるうちに、あっという間に出発時間。朝は本当に一瞬ですね。

なんとか間に合って出社･･･少しだけ達成感です。

そういえば先週、普段あまり行かない場所へ行く機会がありました。
そこで見つけたのが、眼鏡デザインのポスト

システムグラフィのある鯖江市と言えば「眼鏡」
「さすが眼鏡のまち！」と思わず写真を撮ってしまいました！
普段行かないところだったので、こんな発見ができてちょっと嬉しかったです。
（正確にはポストの場所は越前市でした）

いつもの景色もいいですが、少し場所が変わるだけで新しい発見があるものですね。

来週からまたがんばります！
以上　出力yでした。

こんにちは。中日本営業Gの関内です。
いやーびっくりしました。
我が家のＴＶは一般放送が流れなくなって早幾年、仰げば尊し。
卒業式にはまだ少し早い時期ですが。
ＴＶ視聴もめっきり減りましたが、久々にＴＶで一般放送が流れていて、しかもオリンピックが、あぁ、スノーボードかと見始めました。
予選段階とはいえ、男子2位、3位、5位、7位と上位を日本人が押さえているではありませんか。しかも一人は怪我をした直後とか。
女子もすごいですね、高校生がくらいの子たちが飛ぶし、回すし、驚きでした。
且つては・・・スノーボーダーの血を騒がせてくれました。

総務のＭです。

先日、社長からまた飴をいただきました。
またもや巾着からゴソゴソと！！！

その流れで、なぜか「巾着」の話になり、社長の新たな一面を知ることできました！

どうやら巾着がお好きなようで、
旅行に行くときも巾着にまとめているのだとか！

サイズ違いで使い分けているそうで、
整理もしやすいし、繰り返し使えるから無駄も出ない。
自然とSDGsを意識されているところも、さすがだなと思いました。

日々の業務では神経を張りつめることも多いですが、
こうした何気ない会話があると、空気がやわらぎます

 

こんにちは！
出力製作グループのNです！

先日、出力製作グループに新人さんが新しく加わってくれたので、
グループ全員で歓迎会を行いました

お疲れ様です。総務部のコスギです(^^)/

ご紹介が大変遅くなってしまったのですが・・泣

今年も素敵な年賀状を頂きました〜〜


午年の年賀状です！！
将棋の駒の形のフェルトが円の刺繍でしっかり固定されていますよ〜〜




馬の文字は、タオル生地？パイル生地？になっており、ふわふわ・モコモコです〜〜




下地の「新春万福」の印刷の上に、オーガンジー？薄いメッシュのような生地になっており
下の印刷がぼかしがかかっているように見えます！！！！！

素敵です！！！

毎年本当にこのような凝った年賀状を頂き、ありがとうございます！
今年も、机の上に飾っております！

一年間飾って、ものづくりのすばらしさを日々感じたいと思います！！
本当にありがとうございました！！


本年もどうぞ宜しくお願い致します。

以上、総務部のコスギでした(^^)/



西山公園の桜の木　雪が積もってキレイです〜〜



 

こんにちは。
開発営業のTです。

先日、誕生日のお祝いで福井県坂井市にある「三好楼」さんへ行ってきました。

落ち着いた雰囲気のお店で、料理はどれもとても美味しく、特別な日のお食事にぴったりでした。
一品一品が丁寧に作られていて、ゆっくり味わいながら楽しむことができました。

また、お店からの景観も素晴らしく、食事をしながら季節の風景を楽しめるのも魅力のひとつです。
家族での食事はもちろん、記念日やデートなど、さまざまなシーンで利用できるお店だと感じました。

一点だけ注意するとすれば、駐車場が少し分かりづらい点です。
初めて行かれる方は、事前に場所を確認してから向かわれることをおすすめします。

美味しい料理と素敵な時間を過ごせる、また訪れたいお店です。

こんにちは。
東日本営業GのYです。
 
毎日バタバタと過ぎ去っていく中で、先日家族でいつもより少し良い肉を食べに行きました。
向かった先は「平城苑」。店内に一歩足を踏み入れると、独特の落ち着いた高級感が日常を一瞬で忘れさせてくれました。特に、口の中でとろけるような、最高においしい「ザブトン」が印象的でした。
またいけたらいいなぁ・・・。

こんにちは。
西日本営業グループのMです。

宮崎県えびの市付近の高速道路パーキングに立ち寄った時、余りにも綺麗な景色だったので、おもわず写真を撮りました。みな様に共有したいと思います。
自然のグラデーションはなんとも言えない綺麗さです。心が癒されました。