皆さん、こんにちは。システム商品開発グループの入澤です。
秋が深まり朝夕が冷え込む時期になってきました。鯖江の紅葉はもう少し遅くなりそうです。
さて、今回のブログ記事ではプログラマーの仕事の一端を書いてみようと思います。と言ってもプログラミングの話題ではなく高校数学、とくに「直線」に焦点をあてます。数学の基礎中の基礎である直線。グラフィクスに関わる開発では(ベクタ形式のパスを扱うときには尚更)手足のように扱えなければなりません。理由は簡単で、グラフィクスの基本が「線分」だからです。複雑な図形も突き詰めてしまえば線分の連続であって最終的には線分の計算に帰着します。基本的に、線分を直線とみなして計算する場面がほとんど。プログラマーは否が応でも「直線」と向き合うことになるのです。
直線をデータで表す方法はいくつもあり、グラフィクスでは線分を扱うので始点と終点が与えられて、必然的に異なる二点を通る直線を求めることになります。二点の座標さえあれば一応はすべての計算をこなすことは可能なのですが、直線方程式なおかつ陰関数形式 a y + b x + c = 0 の係数を先に計算しておくメリットが多くあります(今回は平面を対象にします)。どのようなメリットがあるか後で書くことにして、まずは二点の座標から直線の係数を計算してみましょう。
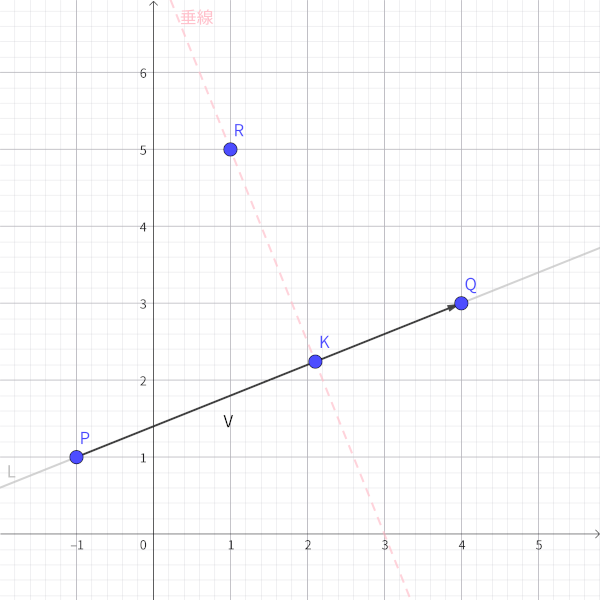
二点 P = ( px , py ) と Q = ( qx , qy ) を通る直線 L は、二点の成すベクトル V = ( qx - px , qy - py ) と直線 L 上の任意の点 ( x , y ) について、外積の性質(平行な二つのベクトルの外積がゼロ)から次の条件を満たすものとして求められます。
( qx - px )( y - py ) - ( qy - py )( x - px ) = 0 .... Eq.1
ここから係数をまとめると次のような数式が得られます。
( qx - px ) y + ( py - qy ) x + ( px qy - qx py ) = 0 .... Eq.2
a = qx - px
b = py - qy
c = px qy - qx py
直線をこのような形式で表すメリットの一つは点と直線の計算にあります。Eq.1 の左辺は、直線 L を表すベクトル V と、点 P から任意の点 ( x , y ) までのベクトル U = ( x - px , y - py ) との外積でしたから、ベクトル V を基準にしてベクトル U の直交成分を符号付きで求めているとみなせます。Eq.2 は Eq.1 の左辺をまとめただけなので、f ( x , y ) = a y + b x + c に調べたい点 R = ( xr , yr ) の座標を代入してゼロと比べるだけで、点 R が直線 L で区切られた左右どちらの半平面にあるか、または線上にあるのかを判定することができます(※この性質は、線分と線分の交差判定にも用いることができます)。
f ( xr , yr ) = a yr + b xr + c > 0 → 点は直線の左側(ベクトル V の向きに対して左側)にある
f ( xr , yr ) = a yr + b xr + c < 0 → 点は直線の右側にある
f ( xr , yr ) = a yr + b xr + c = 0 → 点は直線上にある
加えて、外積の性質(成分が |V| |U| sinθ で求まる)からベクトル V の大きさ |V| で割ることにより、直線から点 ( xr , yr ) までの最短距離 dr を得られるという特性があります。
|V| = √{ (qx - px)2 + (qy - py)2 } = √( a2 + b2 )
dr = f ( xr , yr ) / |V| = ( a yr + b xr + c ) / √( a2 + b2 )
陰関数形式の直線の係数は実数倍に対して自由度があり |V| で割って正規化しておくと、
α = a / √( a2 + b2 )
β = b / √( a2 + b2 )
γ = c / √( a2 + b2 )
g ( x , y ) = α y + β x + γ = 0 ( α2 + β2 = 1 ) .... Eq.3
点と直線の距離を dr = α yr + β xr + γ という単純な計算式で求めることができるようになります。和や積に比べて非常に時間がかかる平方根の計算を最初の一回(係数を求めるときだけ)に抑えられるので高速化につながるというメリットも大きいです。Eq.3 の形式 g ( x , y ) = α y + β x + γ ならば、点 R = ( xr , yr ) の直線 L に対する射影 K = ( xk , yk ) を割り出す計算式
xk = α2 xr - β ( γ + α yr )
yk = β2 yr - α ( γ + β xr )
直線 L1 : α1 y + β1 x + γ1 = 0 と直線 L2 : α2 y + β2 x + γ2 = 0 の交点 S = ( xs , ys ) を割り出す計算式
xs = ( γ1 α2 - γ2 α1 ) / ( α1 β2 - α2 β1 )
ys = ( β1 γ2 - β2 γ1 ) / ( α1 β2 - α2 β1 )
※分母 α1 β2 - α2 β1 = 0 のとき L1 と L2 は平行
などについても(係数6個の四則演算のみで表せるという意味で)比較的単純です。実際には数値計算になるので、浮動小数点数の精度に注意しなければなりませんし、計算誤差による誤判定を見越した堅牢な実装にも気を配ったりと、いかにもプログラマーらしい仕事がもちろん待ち受けているを忘れてはいけません。
以上、長々とお付き合いいただきありがとうございました(タイトルに「その1」と書きましたが、続きがあるかは未定です)。